Gauss’s Law And Its Applications

Electric Charge and Static Electricity

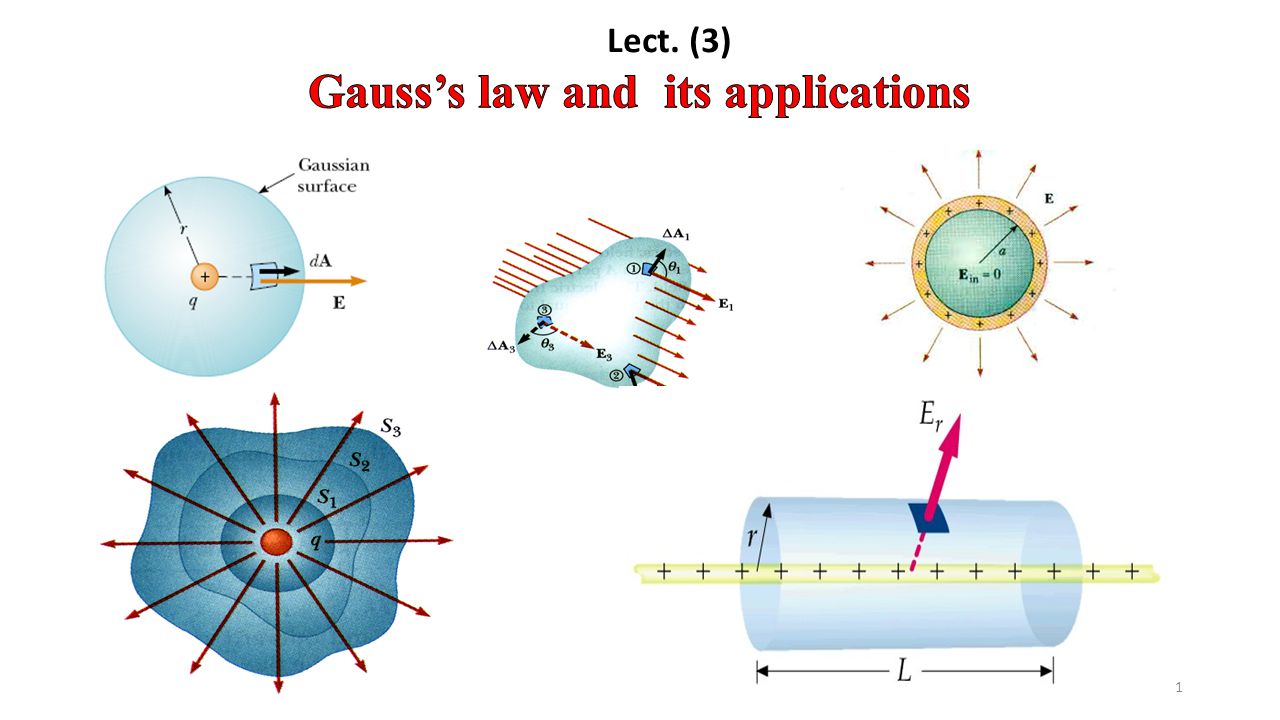
Gauss law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
What Is Gauss Law?
According to Gauss law, the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface.
For example, a point charge q is placed inside a cube of the edge ‘a’. Now, as per Gauss law, the flux through each face of the cube is q/6ε0.
The electric field is the basic concept of knowing about electricity. Generally, the electric field of the surface is calculated by applying Coulomb’s law, but to calculate the electric field distribution in a closed surface, we need to understand the concept of Gauss law. It explains the electric charge enclosed in a closed surface or the electric charge present in the enclosed closed surface.

Gauss Law Formula
As per the Gauss theorem, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. Therefore, if ϕ is total flux and ϵ0 is electric constant, the total electric charge Q enclosed by the surface is
Q = ϕ ϵ0
The Gauss law formula is expressed by
ϕ = Q/ϵ0
Where,
Q = Total charge within the given surface
ε0 = The electric constant
⇒ Also Read: Equipotential Surface

The Gauss Theorem

The net flux through a closed surface is directly proportional to the net charge in the volume enclosed by the closed surface.
Φ = → E.d → A = qnet/ε0
In simple words, the Gauss theorem relates the ‘flow’ of electric field lines (flux) to the charges within the enclosed surface. If no charges are enclosed by a surface, then the net electric flux remains zero.
This means that the number of electric field lines entering the surface equals the field lines leaving the surface.
The Gauss theorem statement also gives an important corollary:
The electric flux from any closed surface is only due to the sources (positive charges) and sinks (negative charges) of the electric fields enclosed by the surface. Any charges outside the surface do not contribute to the electric flux. Also, only electric charges can act as sources or sinks of electric fields. Changing magnetic fields, for example, cannot act as sources or sinks of electric fields.

Electric Field Due to Infinite Wire – Gauss Law Application Consider an infinitely long line of charge with the charge per unit length being λ. We can take advantage of the cylindrical symmetry of this situation. By symmetry, The electric fields all point radially away from the line of charge, and there is no component parallel to the line of charge. We can use a cylinder (with an arbitrary radius (r) and length (l)) centred on the line of charge as our Gaussian surface.